首先开始学习Type-1 fuzzy system (T1 FS), 详细的书中都有,因此这里只从个人理解的方式讲,并非系统学习。T1 FS包括模糊器(Fuzzifier)、推理机(Inference)、规则(Rules)和解模糊器(Defuzzifier)。
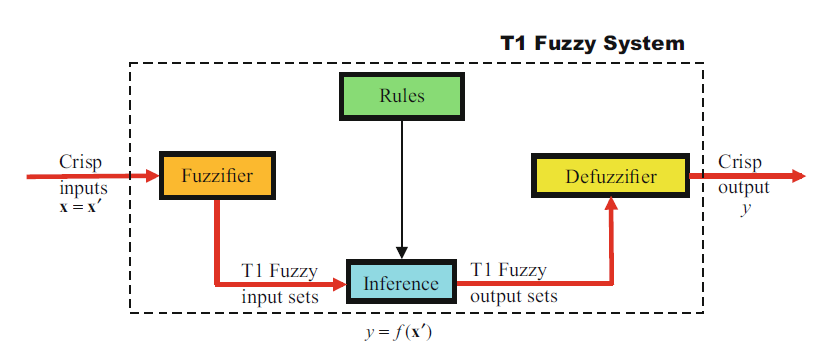
规则 Rules
经典模糊规则包括Zadeh规则和TSK规则,考虑一个模糊系统具有 $p$ 个输入$x_{1} \in X_{1}, \ldots, x_{p} \in X_{p}$(就是说$\mathbf{x}$的维度是$p$)和一维输出$y \in Y$,两种模糊规则定义如下:
定义 3.1a 针对Zadeh规则下的模糊系统,其中第$l$个$(l=1, \ldots, M)$通用Zadeh规则定义为:
这里的$F_{p}^{l}$是指第$l$条规则在第$p$维度上的模糊集,输出$G^{l}$是一型模糊集,可以由其隶属度函数(MF)定义:$\mu_{G^{l}}(y)$
定义 3.1b 针对TSK规则下的模糊系统,其中第$l$个$(l=1, \ldots, M)$通用TSK规则定义为:
这TSK规则中的输出是清晰数,当然,也可以认为是模糊单值(fuzzy singleton)。注意:使用Zadeh规则的模糊系统称为Mamdani模糊系统,使用TSK模糊规则的模糊系统称为TSK模糊系统。
模糊器 Fuzzifier
模糊器将清晰值(crisp point)$\mathbf{x}=\left(x_{1}, \ldots, x_{p}\right)^{T} \in X_{1} \times X_{2} \times \cdots \times X_{p} \equiv \mathbf{X}$映射到模糊集$A_{\mathrm{x}}$ in $\mathbf{X}$。
定义 3.4 单值模糊器(singleton fuzzifier) 是指$\mu_{X_{i}}\left(x_{i}^{\prime}\right)=1$且对于 $x_{i} \in X_{i}$ , $x_{i} \neq x_{i}^{\prime}$情况,$\mu_{X_{i}}\left(x_{i}\right)=0$ 。(也就是说,只有一个位置隶属度为1,其他都为零)。
定义 3.4 非单值模糊器(non-singleton fuzzifier) 是指对于清晰观测值$x_{i}=\mathrm{x}_{i}^{\prime}$,映射成一个一型模糊数,在观测值位置隶属度为1,远离观测值的位置隶属度逐步下降。即为:$\mu_{X_{i}}\left(x_{i}^{\prime}\right)=1$,其他位置隶属度表示为$\mu_{X_{i}}\left(x_{i} | x_{i}^{\prime}\right)$
隶属函数常用的有高斯和三角两种:
1.高斯隶属函数: $\mu_{X_{i}}\left(x_{i} | x_{i}^{\prime}\right)=\exp \left[-x_{i}-x_{i}^{\prime}\right)^{2} / 2 \sigma^{2} ]$
2.三角隶属函数: $\mu_{X_{i}}\left(x_{i} | x_{i}^{\prime}\right)=\max \left(0,1-\left|\left(x_{i}-x_{i}^{\prime}\right) / c\right|\right)$
高斯隶属度中的$x_{i}^{\prime}$指模糊集的中心,即为观测值的清晰数,$\sigma$是模糊集的伸展度,因此高斯隶属度可以理解为把一个清晰数描述成带噪声的数,这个$\sigma$可以理解为噪声的范围。
模糊推理机 Fuzzy inference Engine
规则输出
首先从Mamdani模糊系统开始:令$F_{1}^{l} \times \cdots \times F_{p}^{l}=A^{l}$(其中$A^{l}$是$\mathbf{x}$的模糊集,$F_{p}^{l}$是指第$l$条规则在第$p$维度上的模糊集,$\times$指模糊集之间的运算符), Mamdani FS表示为:
规则$R_{Z}^{l}$由隶属函数$\mu_{R_{Z}^{l}}(\mathbf{x}, y)$所描述(注意这个隶属函数是描述规则的真值度,也就是规则的成立程度,与之前的隶属函数的意义是不同的):
$p$个维度的规则隶属度之间可以用T-范运算,简写为T:
其中$\star$是指T-范运算,可以是取最小或者取乘积。也被称作Mamdani蕴含(Mamdani implication)
$p$个维度的输入隶属度为:
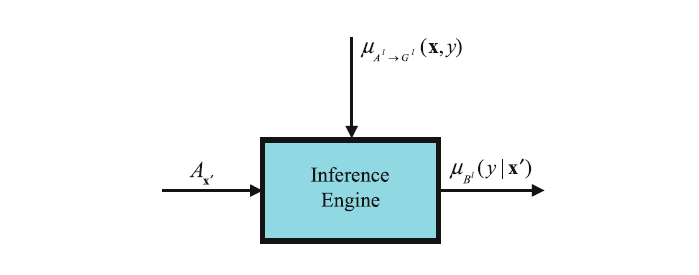
每条规则$R_{Z}^{l}$都决定了一个输出模糊集$B^{l}=A_{\mathbf{x}^{\prime}} \circ R_{Z}^{l}$,$B^{l}$由其隶属度表示:
隶属度用类似条件概率的方式表达,是因为输出的隶属度是$\mathbf{x}^{\prime}$的函数。其中$\star$是指T-范运算,sup[ ] 称作 sup-star composition 是取T-范之后的上界,可以这么认为:把sup[ ]中的两个元素写成矩阵,加法处理编程取最大值运算。
式子3.10中的两个隶属度分别可以表示成$p$维的形式,也就是式3.8和式3.9。带入3.11可得:
就是说输出规则是由多个上确界与输出隶属函数的T-范。
上式中大括号之内的称作第$l$条规则的‘火力范围’定义成$
f^{l}\left(\mathbf{x}^{\prime}\right) \in[0,1]$:
这里的火力范围是$\mathbf{x}^{\prime}$的函数,计算之后其实是个常数。对$\mathbf{x}^{\prime}$进行降维表示为:
此时式3.12可以简化为:
式子3.11可以化简为:
所以说一个规则的输出其实就是一个规则的火力范围与其后件模糊集的T-范运算。
总结一下,Mamdani模糊系统和TSK模糊系统的规则输出分别为:
请注意,Mamdani模糊系统的输出是火力范围运算后件,其后件是个模糊集,而TSK模糊系统的后件是个线性模型,是个清晰数,后面会说明区别。
详解推理机
现在举例详细理解一下推理机,一型单值情况比较简单,这里关注一型非单值的情况。
首先看第$i$个维度上,假如第$l_1$个规则的中心为$c_1$,对于观测点$x_i$,火力范围可以表述为:
看下图,在取sup之前两个隶属函数的运算结果为粗线,根据T-范取最小还是乘积,粗线结果如下图a和b,对粗线进行取sup就是取粗线最高的位置,观测值在每个规则每个维度上都会有火力范围,如下图a,对于规则$l_1$,火力范围为:
同理:
在T-范取乘积的时候,粗线不一样,sup结果也不一样,如图b,火力范围分别为0.6和0.4。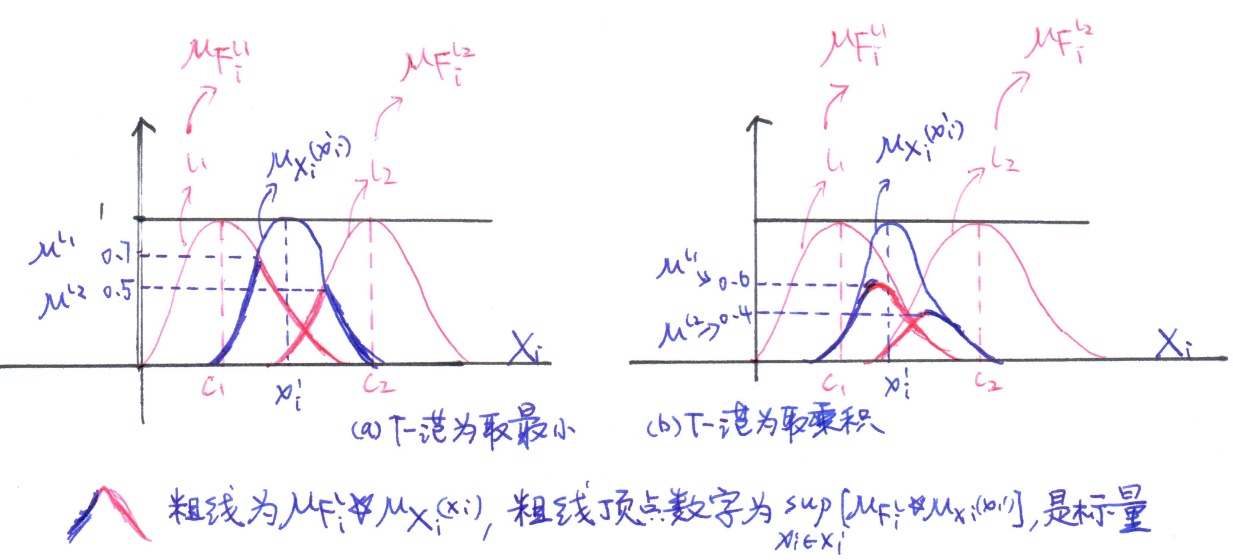
当然到这只是得到了观测值在每个规则在每个维度下的火力范围,$p$个维度的火力运算之后形成一个火力值,当然这个运算可以用相乘也可以取最小,对于每个规则,最终得到一个运算之后的火力范围$u^{l}$,如图,其实就是$f^{l}\left(\mathbf{x}^{\prime}\right)$,是个常数。根据公式3.13,对于Mamdani模糊系统,每个规则的最终火力范围还需要与此规则的输出隶属函数进行运算,如图3.6,虚线是输出的模糊集(隶属函数),红线是每个规则的最终火力范围,这里运算也可以取最小或乘积,分别对于下图a和b中的粗黑线。
至此,我们得到了观测点在每条规则下的输出,都是模糊数。
所以对于Mamdani模糊系统,每个规则的后件是一个带不确定度的$y$,也就是一个模糊集,而对于TSK模糊系统,每个规则的后件是一个线性确定模型,两种模糊系统的后件经过点火之后,都具有很强的拟合能力。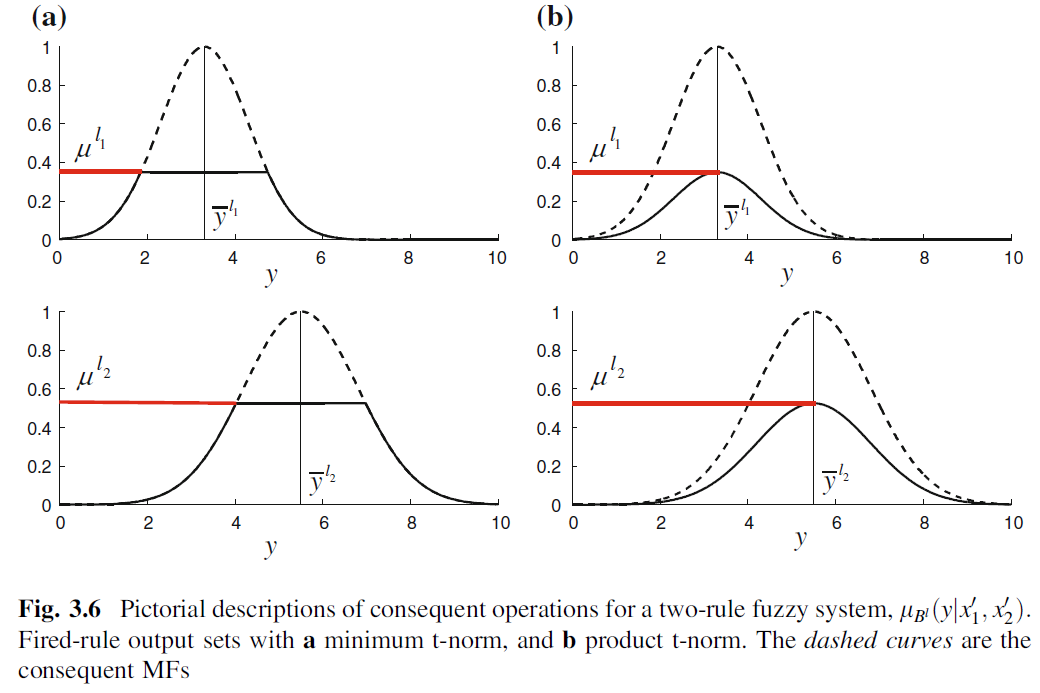
再回到Mamdani系统,当我们得到每个规则的输出模糊集之后,如何连接规则呢,因为我们最终需要的是个清晰的输出,所以可以先对每个规则解模糊化之后再连接规则,也可以先连接模糊规则再解模糊化,如下图,就是先连接了两条模糊规则,得到总输出模糊集,图中虚线是后件,经过点火之后变矮了一点,两个规则的连接后规则即为实线。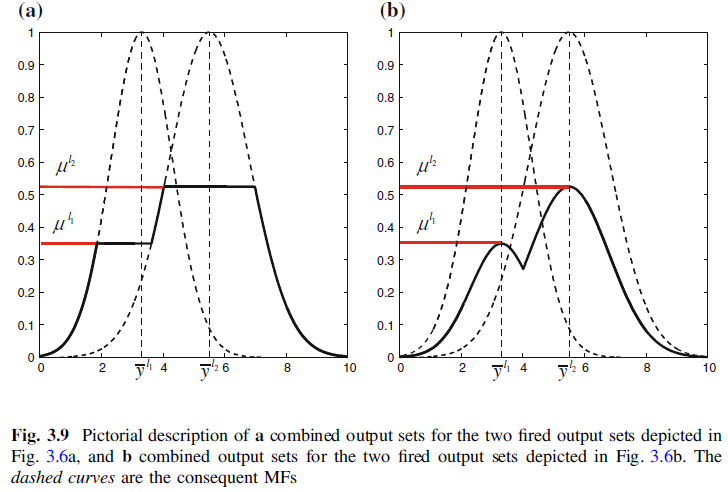
不同规则输出之间也可以加权连接,这个权重可以以某些方法预设,也可以通过梯度下降训练,如下图: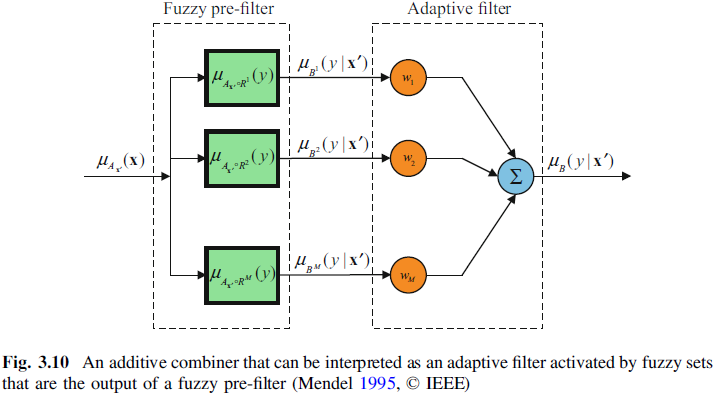
解模糊器 Defuzzifier
TSK模糊系统输出只是火力范围和线性输出的加权和,只有Mamdani模糊系统才需要解模糊。解模糊的方法有重心解模糊器(Centroid Defuzzifier)、高度解模糊器(Height Defuzzifier)、集中心解模糊器(COS),以COS为例,首先将每个后件替换成重心的单值,其高度等于点火水平,然后找出这些单值构成的一型模糊集的重心。
如图,每个红色箭头横坐标为后件的中心位置,纵坐标为后件的高度,求出这些箭头点重心的位置的横坐标,作为解模糊的输出。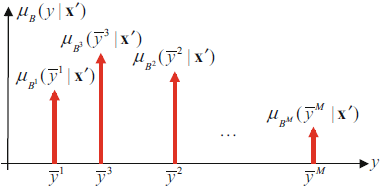
总结
目前最常用的模糊系统是一型单值TSK模糊系统,一型/二型,单值/非单值,TSK/Mamdani都值得探索,这些模糊系统都是万能逼近器,其求解方式可以是最小二乘、梯度下降、SVD等等,下一节我若有时间则学习学习。其实模糊系统性能是很强的,只是没有神经网络简单易懂,扩展起来过于复杂,因此没有其他算法火爆。
同时,模糊系统的模糊化过程,与概率分布有异曲同工之妙。
王鹏程是傻逼