TSK Tranfer learning

  两个研究小组都聚焦于TSK模糊系统下的迁移学习，因此仔细研究一下 TSK Fuzzy system 下的 Transfer learning。
文章附图，挺复杂的，暂时没看懂：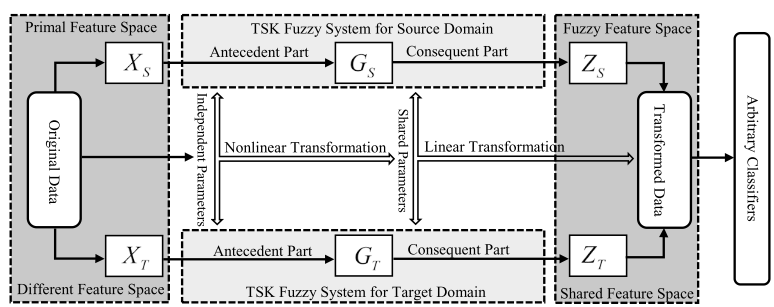

---

TSK Fuzzy Logis System

TSK模糊模型由一组简单的模糊推理规则构成：

$$\begin{array}{l}{\text { IF } \quad x_{1} \text { is } A_{1}^{k} \wedge x_{2} \quad \text { is } A_{2}^{k} \wedge \ldots \wedge x_{d} \quad \text { is } A_{d}^{k}} \\ {\text { Then } f^{k}(\mathbf{x})=p_{0}^{k}+p_{1}^{k} x_{1}+p_{2}^{k} x_{2}+\cdots+p_{d}^{k} x_{d}} \\ {k=1,2, \ldots, K}\end{array} \tag{1}$$

其中$x_{j},(j=1,2, \dots, d)$下标是输入的第$j$个维度，$d$是输入的总维度，$K$是模糊规则的总数量。$f^{k}(\boldsymbol{x})$是第$k$个模糊规则下的输出。输入空间上的模糊集$A^{k} \subset R^{d}$被映射到输出空间上$f^{k}(x) \subset R$上。$\wedge$是模糊并运算。请注意这个$f^{k}(x)$只是一个模糊规则的输出，二TSK是多个模糊规则下的输出：

$$y=\sum_{k=1}^{K} \frac{\mu^{k}(\mathbf{x})}{\sum_{k^{\prime}=1}^{K} \mu k^{\prime}(\mathbf{x})} f^{k}(\mathbf{x})=\sum_{k=1}^{K} \tilde{\mu}^{k}(\mathbf{x}) f^{k}(\mathbf{x})=\sum_{k=1}^{K} \tilde{\mu}^{k}(x)\left(p_{0}^{k}+p_{1}^{k} x_{1}+\cdots+p_{d}^{k} x_{d}\right)$$

式中$\mu^{k}(\mathbf{x})$是模糊集$A^{k}$的隶属度值，$\tilde{\mu}^{k}(\mathbf{x})$是正则化之后的隶属度。请注意模糊集$A^{k}$的维度是$d$，$\mathbf{X}$的隶属度是每个维度的隶属度的乘积：

$$\mu^{k}(\mathrm{x})=\prod_{i=1}^{d} \mu_{A_{i}^{k}}\left(x_{i}\right)$$

其中$\mathbf{X}$每个维度的隶属度值可以由有多种模型，如三角隶属度或者高斯隶属度。此处选择高斯隶属度：

$$\mu_{A_{i}^{k}}\left(x_{i}\right)=\exp \left(\frac{-\left(x_{i}-c_{i}^{k}\right)^{2}}{2 \delta_{i}^{k}}\right) \tag{2}$$

高斯隶属度的中心值$c_{i}^{k}$和宽度值$\delta_{i}^{k}$可以由多种方法确定，此处选择Fuzzy c-means方法求解。这个方法程序可以轻松在网上找到。两个参数可以表示为：

$$c_{i}^{k}=\frac{\sum_{j=1}^{N} u_{j k} x_{j i}}{\sum_{j=1}^{N} u_{j k}}$$ $$\delta_{i}^{k}=\frac{h \cdot \sum_{j=1}^{N} u_{j k}\left(x_{j i}-c_{i}^{k}\right)^{2}}{\sum_{j=1}^{N} u_{j k}}$$

式中$u_{j k}$是值第$k$个聚类下的第$j$个样本的隶属度。$N$是样本总数量。TSK加上FCM算法下，聚类中心的数量即为模糊规则的数量。$h$是模型超参数，可以用交叉验证等策略确定。
经过以上过程得到训练数据的隶属度之后，多个维度的隶属度为每个维度隶属度相乘：

$$\mu^{k}(\mathbf{x})=\prod_{i=1}^{d} \mu_{A_{i}^{k}}\left(x_{i}\right) \tag{3}$$

隶属度函数正则化：

$$\tilde{\mu}^{k}(\mathbf{x})=\mu^{k}(\mathbf{x}) / \sum_{k^{\prime}=1}^{K} \mu^{k^{\prime}}(\mathbf{x}) \tag{4}$$

此时FS的输出是：

$$f(\mathbf{x})=\sum_{k=1}^{K} \tilde{\mu}^{k}(\mathbf{x}) f^{k}(x) \tag{5}$$

到此隶属度虽然有了，但是每个$f^{k}(x)$中仍有未知参数$p_{d}^{k}$。
接着，FS的输出可以简化为：

$$y=f(\mathbf{x})=\mathbf{p}_{g}^{\mathrm{T}} \mathbf{x}_{g} \tag{6}$$

其中输入加上偏置：

$$\mathbf{x}_{e}=\left[1, \mathbf{x}^{\mathrm{T}}\right]^{\mathrm{T}} \in R^{(d+1) \times 1} \tag{7a}$$

每个子规则的输入乘隶属度，之后再乘线性模型参数p，以下处理只是为了计算方便：

$$\tilde{\mathbf{x}}^{k}=\tilde{\mu}^{k}(\mathbf{x}) \mathbf{x}_{e} \in R^{(d+1) \times 1} \tag{7b}$$ $$\mathbf{x}_{g}=\left[\left(\tilde{\mathbf{x}}^{1}\right)^{\mathrm{T}},\left(\tilde{\mathbf{x}}^{2}\right)^{\mathrm{T}}, \cdots,\left(\tilde{\mathbf{x}}^{K}\right)^{\mathrm{T}}\right]^{\mathrm{T}} \in R^{K(d+1) \times 1} \tag{7c}$$ $$\mathbf{p}^{k}=\left[p_{0}^{k}, p_{1}^{k}, \cdots, p_{d}^{k}\right]^{\mathrm{T}} \in R^{(d+1) \times 1} \tag{7d}$$ $$\mathbf{p}_{g}=\left[\left(\mathbf{p}^{1}\right)^{\mathrm{T}},\left(\mathbf{p}^{2}\right)^{\mathrm{T}}, \cdots,\left(\mathbf{p}^{K}\right)^{\mathrm{T}}\right]^{\mathrm{T}} \in R^{K(d+1) \times 1} \tag{7e}$$

经过以上处理之后，$\mathbf{X}_{g}$即为经过Fuzzy 映射之后的特征向量，其实就是原数据乘以隶属度，文中称作：_the antecedent part of TSK-FS_ 。 而后面的参数部分$\mathbf{p}_{g}$文中称作：_the consequent parameters of the TSK-FS_ 。此时由于隶属度全是已知的，式子(6)其实是一个线性模型，在输入给定时，可以用最小二乘法求解$\mathbf{p}_{g}$。

Maximum Mean Discrepency

文中又回顾了以下最大均值偏差，这里不详细说了：

$$\operatorname{MMD}^{2}(\mathbf{X}, \mathbf{Y})=\left\|\frac{1}{m} \sum_{i=1}^{m} \phi\left(\mathbf{x}_{i}\right)-\frac{1}{n} \sum_{j=1}^{n} \phi\left(\mathbf{y}_{j}\right)\right\|_{\mathcal{H}}^{2} \tag{8}$$

迁移学习的目的是求解$\phi$。[_这么说勉强也可以_]
然后作者觉得需要同时对齐边缘和条件分布，因此采用了清华龙组的JDA方法，首先边缘和条件分布分别表示为：

$$\operatorname{MMD}_{P}^{2}\left(\mathbf{X}_{s}, \mathbf{X}_{T}\right)=\left\|\frac{1}{n_{s}} \sum_{i=1}^{n_{n}} \phi\left(\mathbf{x}_{s_{i}}\right)-\frac{1}{n_{t}} \sum_{j=1}^{n_{n}} \phi\left(\mathbf{x}_{t_{j}}\right)\right\|_{\mathcal{H}}^{2} \tag{9a}$$ $$\operatorname{MMD}_{Q}^{2}\left(\mathbf{X}_{S}, \mathbf{X}_{T}\right)=\sum_{c=1}^{C}\left\|\frac{1}{n_{s}^{(c)}} \sum_{y_{i_{i}=c}} \phi\left(\mathbf{x}_{s_{i}}\right)-\frac{1}{n_{t}^{(c)}} \sum_{\hat{y}_{i j}=c} \phi\left(\mathbf{x}_{t_{j}}\right)\right\|_{\mathcal{H}}^{2} \tag{9b}$$

这里对于条件分布的表示略微奇怪，不过没关系，先继续看。其中$C$是分类问题对应的总类别。$n_{s}^{(c)}$是原数据中对应于类别$c$的样本的个数。目标数据集的伪标签是基于原数据训练的，初始伪标签精度较低，后续会不断迭代，这些在JDA方法中都有，我先继续看看作者还要做什么。

Overview of TRL-TSK-FS

Transfer representation learning - TSK- Fuzzy system. 为了在缩小分布距离的同时保证数据结构，目标函数定义如下：

$$\min _{\phi} D i s t a n c e\left(\mathbf{X}_{S}, \mathbf{X}_{T} | \phi\right)+\operatorname{Info}_{-} \operatorname{loss}\left(\mathbf{X}_{s}, \mathbf{X}_{T} | \phi\right) \tag{10}$$

Shared Feature Space Construction

_通常构建特征空间的方式为：首先非线性变换，再降维 — 作者_
文章的创新思路在于对于 _the antecedent part_ 做非线性变换，再对 _the consequent part_ 做降维。
回顾以下，前者是指乘了隶属度之后的训练样本，后者参数是线性子模型的参数p，这里把多输出TSK-FS的输出当作了是输出特征，因此本文其实是把MO-TSK-FS当作了自编码器，。

Fuzzy feature space based on TSK-FS

源数据和目标数据上的单个样本分别表示为：

$$\mathbf{g}_{s_{i}}=\left[\left(\tilde{\mathbf{x}}_{s_{i}}^{1}\right)^{\mathrm{T}},\left(\tilde{\mathbf{x}}_{s_{i}}^{2}\right)^{\mathrm{T}}, \cdots,\left(\tilde{\mathbf{x}}_{s_{i}}^{K}\right)^{\mathrm{T}}\right]^{\mathrm{T}} \in R^{K(d+1) \times 1} \tag{11a}$$ $$\mathbf{g}_{t_{i}}=\left[\left(\tilde{\mathbf{x}}_{t_{i}}^{1}\right)^{\mathrm{T}},\left(\tilde{\mathbf{x}}_{t_{i}}^{2}\right)^{\mathrm{T}}, \cdots,\left(\tilde{\mathbf{x}}_{t_{i}}^{K}\right)^{\mathrm{T}}\right]^{\mathrm{T}} \in R^{K(d+1) \times 1} \tag{11b}$$

整个源数据集和目标数据集表示为：

$$\mathbf{G}_{S}=\left[\mathbf{g}_{s_{1}}, \mathbf{g}_{s_{2}}, \cdots, \mathbf{g}_{s_{n_{s}}}\right] \in R^{K(d+1) \times n_{s}} \tag{11c}$$ $$\mathbf{G}_{T}=\left[\mathbf{g}_{t_{1}}, \mathbf{g}_{t_{2}}, \cdots, \mathbf{g}_{t_{l_{n}}}\right] \in R^{K(d+1) \times n_{i}} \tag{11d}$$

模型参数P此处乘以了m，整个FS变成了多输出FS：

$$\mathbf{P}=\left[\mathbf{p}_{g}^{1}, \mathbf{p}_{g}^{2}, \cdots, \mathbf{p}_{g}^{m}\right] \in R^{K(d+1) \times m} \tag{11e}$$

本来FS是一个向量$\mathbf{x}$映射到一个$y$数字，现在变成了一个向量$\mathbf{x}$映射到m个数字$y$，于是多输出的FS变成了一个从向量$\mathbf{x}$到向量$\mathbf{y}$的映射，如果后者的维度低于前者，那么就可以当作是一种降维提取高级特征。我觉得这种方法优点问题
继续看，对于一个样本$\boldsymbol{g}_{s_{i}}$，映射表示为：

$$\phi\left(\mathbf{x}_{s_{i}}\right)=\mathbf{P}^{\mathrm{T}} \mathbf{g}_{s_{i}} \tag{12a}$$ $$\phi\left(\mathbf{x}_{t_{i}}\right)=\mathbf{P}^{\mathrm{T}} \mathbf{g}_{t_{i}} \tag{12b}$$

对于整组源数据和目标数据，映射可以表示为：

$$\mathbf{Z}_{S}=\mathbf{P}^{\mathrm{T}} \mathbf{G}_{S} \tag{13a}$$ $$\mathbf{Z}_{T}=\mathbf{P}^{\mathrm{T}} \mathbf{G}_{T} \tag{13a}$$

疑问：一般特征表示及降维，所得到的特征是正交的。而这里多输出很有可能多个模糊输出是相同的
文中这里假设源数据和目标数据都服从一组参数P，也就是服从相同的线性模糊模型
总结：文章认为，源数据和目标数据的隶属度是不同的，而模糊规则是相同的，翻译成文中的话就是，前参数相同，而后参数是不同的。源数据和目标数据的前参数[中心值和宽度值]可以通过FCM求解。而后参数则是基于JDA的方法优化。

Antecedent parameters (前参数即隶属度等)

FCM 虽然常用，但是却不稳定，对参数非常敏感，此处使用了 Var-Part聚类方法。用于得到前参数中的聚类中心和聚类宽度，从而计算隶属度。

   T. Su and J. G. Dy, "In search of deterministic methods for initializing K-means and Gaussian mixture clustering," Intelligent Data Analysis, vol. 11, pp. 319-338, 2007

Distribution Matching

此处开始用JDA的方法，因此简写：
最小化边缘分布：

$$\operatorname{MMD}_{P}^{2}\left(\mathbf{Z}_{S}, \mathbf{Z}_{T}\right)=\left\|\frac{1}{n_{s}} \sum_{i=1}^{n_{s}} \mathbf{P}^{\mathrm{T}} \mathbf{g}_{s_{i}}-\frac{1}{n_{t}} \sum_{j=1}^{n_{i}} \mathbf{P}^{\mathrm{T}} \mathbf{g}_{t_{j}}\right\|_{\mathcal{f}}^{2}=\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{G}_{X} \mathbf{M} \mathbf{G}_{X}^{\mathrm{T}} \mathbf{P}\right) \tag{15}$$

最小化条件分布：

$$\operatorname{MMD}_{Q}^{2}\left(\mathbf{Z}_{S}, \mathbf{Z}_{T}\right)=\sum_{c=1}^{C}\left\|\frac{1}{n_{s}^{(c)}} \sum_{y_{s_{i}}=c} \mathbf{P}^{\mathrm{T}} \mathbf{g}_{s_{i}}-\frac{1}{n_{t}^{(c)}} \sum_{\hat{y}_{t_{i}}=c} \mathbf{P}^{\mathrm{T}} \mathbf{g}_{t_{i}}\right\|_{\mathcal{H}}^{2} =\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{G}_{X} \sum_{c=1}^{C} \mathbf{M}_{c} \mathbf{G}_{X}^{\mathrm{T}} \mathbf{P}\right) \tag{16}$$

总优化目标即为：

$$\min _{\mathbf{P}} \operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{G}_{X} \mathbf{M} \mathbf{G}_{X}^{\mathrm{T}} \mathbf{P}\right)+\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{G}_{X} \sum_{c=1}^{c} \mathbf{M}_{c} \mathbf{G}_{X}^{\mathrm{T}} \mathbf{P}\right) \tag{17}$$

式10需要求解映射$\phi$，而式17只需要求解线性映射P，这就是本文的创新，其实优点像TCA文中，也不求解映射，只是假设是某种映射。

保持数据几何结构

这部分其实就是TCA中用到的，最大化中心矩阵方差的形式，保持数据结构：

$$\max _{\mathbf{P}} \operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{G}_{T} \mathbf{H}_{T} \mathbf{G}_{T}^{\mathrm{T}} \mathbf{P}\right) \tag{18}$$

其中$\mathbf{H}_{T}$是中心矩阵。
同时考虑the discriminant information，作者又丰富了目标函数，这个我没见过，可能是一种常用的保持数据类别结构的方法吧：

$$\min _{\mathbf{P}} \frac{\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{S}_{w} \mathbf{P}\right)}{\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{G}_{T} \mathbf{H}_{T} \mathbf{G}_{T}^{\mathrm{T}} \mathbf{P}\right)+\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{S}_{b} \mathbf{P}\right)} \tag{22}$$

联合优化目标

$$\min _{\phi} D i s t a n c e\left(\mathbf{X}_{S}, \mathbf{X}_{T} | \phi\right)+\operatorname{Info}_{-} \operatorname{loss}\left(\mathbf{X}_{S}, \mathbf{X}_{T} | \phi\right)$$ $$=\min _{\mathbf{P}} \frac{\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{G}_{X}\left(\mathbf{M}+\sum_{c=1}^{C} \mathbf{M}_{c}\right) \mathbf{G}_{X}^{\mathrm{T}} \mathbf{P}\right)+\alpha \operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{P}\right)+\beta \operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{S}_{w} \mathbf{P}\right)}{\lambda \operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{G}_{T} \mathbf{H}_{T} \mathbf{G}_{T}^{\mathrm{T}} \mathbf{P}\right)+\beta \operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}} \mathbf{S}_{b} \mathbf{P}\right)}$$ $$=\min _{\mathbf{p}} \frac{\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}}\left(\mathbf{G}_{X}\left(\mathbf{M}+\sum_{c=1}^{c} \mathbf{M}_{c}\right) \mathbf{G}_{X}^{\mathrm{T}}+\alpha \mathbf{I}+\beta \mathbf{S}_{w}\right) \mathbf{P}\right)}{\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}}\left(\lambda \mathbf{G}_{\tau} \mathbf{H}_{T} \mathbf{G}_{T}^{\mathrm{T}}+\beta \mathbf{S}_{b}\right) \mathbf{P}\right)} \tag{23}$$

$\alpha, \beta$ and $\lambda$是正则化参数，与JDA求解相似，转成约束优化问题：

$$\min _{P} \operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}}\left(\mathbf{G}_{X}\left(\mathbf{M}+\sum_{c=1}^{c} \mathbf{M}_{c}\right) \mathbf{G}_{X}^{\mathrm{T}}+\alpha \mathbf{I}+\beta \mathbf{S}_{w}\right) \mathbf{P}\right)$$ $$s.t. \ \operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}}\left(\lambda \mathbf{G}_{T} \mathbf{H}_{T} \mathbf{G}_{T}^{\mathrm{T}}+\beta \mathbf{S}_{b}\right) \mathbf{P}\right)=1 \tag{24}$$

上式可以用拉格朗日方程表示为：

$$L=\operatorname{Tr}\left(\mathbf{P}^{\mathrm{T}}\left(\mathbf{G}_{X}\left(\mathbf{M}+\sum_{c=1}^{C} \mathbf{M}_{c}\right) \mathbf{G}_{X}^{\mathrm{T}}+\alpha \mathbf{I}+\beta \mathbf{S}_{w}\right) \mathbf{P}\right)$$ $$+\operatorname{Tr}\left(\left(\mathbf{P}^{\mathrm{T}}\left(\lambda \mathbf{G}_{T} \mathbf{H}_{T} \mathbf{G}_{T}^{\mathrm{T}}+\beta \mathbf{S}_{b}\right) \mathbf{P}-\mathbf{I}\right) \Phi\right) \tag{25}$$

其中$\Phi=\operatorname{diag}\left(\varphi_{1}, \varphi_{2}, \cdots, \varphi_{m}\right) \in R^{m \times m}$是拉格朗日乘子，使$\frac{\partial L}{\partial \mathbf{P}}=0$可得：

$$\left(\mathbf{P}^{\mathrm{T}}\left(\mathbf{G}_{X}\left(\mathbf{M}+\sum_{c=1}^{C} \mathbf{M}_{c}\right) \mathbf{G}_{X}^{\mathrm{T}}+\alpha \mathbf{I}+\beta \mathbf{S}_{w}\right) \mathbf{P}\right)$$ $$=\left(\lambda \mathbf{G}_{T} \mathbf{H}_{T} \mathbf{G}_{T}^{\mathrm{T}}+\beta \mathbf{S}_{b}\right) \mathbf{P} \Phi \tag{26}$$

到这里是个广义特征值分解问题，可以用matlab的eigs直接求解了！

计算复杂度

刚好JDA文章有计算复杂度分析，这里完全复刻过来就行。

总结

本文的创新在于，利用模糊模型做假设：源数据和目标数据仅隶属度不同，而模糊规则相同。不管这种假设是否成立，这毕竟是一种新的思路。很棒。

[1]Yang C, Deng Z, Choi K S, et al. Takagi–Sugeno–Kang transfer learning fuzzy logic system for the adaptive recognition of epileptic electroencephalogram signals[J]. IEEE Transactions on Fuzzy Systems, 2016, 24(5): 1079-1094.
[2] Zuo H, Zhang G, Pedrycz W, et al. Fuzzy regression transfer learning in Takagi–Sugeno fuzzy models[J]. IEEE Transactions on Fuzzy Systems, 2017, 25(6): 1795-1807.
[3] Xu P, Deng Z, Wang J, et al. Transfer Representation Learning with TSK Fuzzy System[J]. arXiv preprint arXiv:1901.02703, 2019.