Fuzzy System

  在做Fuzzy Transfer 之前，一周时间学习一下Fuzzy System。其目的是了解Fuzzy部分在他人研究中到底占据多少的创新。
  模糊系统基于模糊逻辑,与传统的二值逻辑相比，模糊逻辑更加接近于人类的思维和自然语言。原理上，模糊逻辑提供了一种有效的方式来获取现实世界中近似的和不精确的特性。一个模糊系统中基本的部分是一个语言规则集，该规则间通过模糊蕴涵和推理式的合成规则这两个概念相关联。本质上，模糊系统提供了一种很烦，即把基于专家知识的语言规则转换成自动的控制行为。许多实验表面模糊系统得出的结果远远优于用传统方法得到的结果。特别是当用传统的定量方法分析起来太复杂，或者当已知的信息源只能定性地、不精确地或不确定地描述时，模糊系统方法显得非常有效。因此，可以认为模糊系统朝着传统的精确数学方法和人类决策的最终交融靠近了一步。

-- 本篇文章大部分内容来自教材《 Matlab模糊系统设计》

---

模糊集

 模糊集是传统的集合论的推广，该集合中包含隶属于不精确的元素。把隶属的程序定义为隶属度函数(Menbership funtion)，通常该函数是一个位于0~1之间的数值。这种方法明确地提供了一种用于数学模型表达不确定性的方法。通常来说，两个用的最广泛的隶属度描述为三角函数和高斯函数，他们的定义如下：

• 三角隶属函数 $$\mu(x)=\left\{\begin{array}{cc}{1-\frac{|x-m|}{\sigma},|x-m| \leqslant \sigma} \\ {0, \qquad Other}\end{array}\right.$$   式中： $m, \sigma $分别是该模糊集的中心和宽度。
• 高斯隶属度函数

$$\mu(x)=\exp \left[-\frac{(x-c)^{2}}{\sigma^{2}}\right]$$

  式中$c, \sigma $分别是高斯模糊集的中心和宽度

---

模糊规则

  模糊系统本质上是一个基于规则的专家系统，它包括一组“IF-THEN”形式的语言规则。到目前位置，最常用的模糊规则是纯粹的模糊模型（或者模糊IF-THEN规则）以及TSK模型。

1 模糊IF-THEN规则

  模糊IF-THEN规则也称为模糊蕴涵或模糊条件描述，他们都是用IF A THEN B的形式的语句来表示的。由于他们的形式简单，模糊IF-THEN 语句通常用于表达不精确的推理方式，这种推理方式对于人们在不确定或不精确环境下仍然具有做出决策的能力上起着非常重要的作用。一个普遍的例子如下：

$$R^{i} : \operatorname{IF} x_{1} \text { is } F_{1}^{i} \text { and } \cdots \text { and } x_{r} \text { is } F_{r}^{i}, \text { THEN } y_{1} \text { is } G_{1}^{i} \text { and } \cdots \text { and } y_{s} \text { is } G_{s}^{i}$$

  其中:$F_{j}^{i}(j=1,2, \cdots, r), \quad G_{k}^{i}(k=1,2, \cdots, s)$是模糊集的标识，他们用适当的隶属度函数来刻画； $X=\left(x_{1}, x_{2}, \cdots, x_{r}\right) \in \mathbf{R}^{r}, \quad Y=\left(y_{1}, y_{2}, \cdots, y_{s}\right) \in \mathbf{R}^{s}$分别为语言变量的输入和输出；上标$i(=1,2, \cdots, u)$表示第$i$条规则。

  每一个模糊IF-THEN规则定义了一个模糊集:

$$F_{1}^{i} F_{2}^{i} \cdots F_{r}^{i} \rightarrow G_{1}^{i} G_{2}^{i} \cdots G_{s}^{i}$$

由于多输入-多输出(MIMO)的规则都是相互独立的，因此MIMO模糊系统的一般规则结构都可以表示为多输入-单输出(MISO)模糊系统。之所以可以这样，是因为可以根据$G_{k}^{i}(k=1,2, \cdots, s)$把以上的规则分解成$s$个子规则，并以此作为第$i$个子规则的独立结果。
为了陈述简单，在下面的分析中将仅考虑多输入-单输出系统。

  模糊IF-THEN系统组成了模糊逻辑系统的基本部分，它是一个普遍的加工，在这个架构中，来自于人类专家的语言信息被量化，同时模糊逻辑的法则使得这个语言信息能够被系统利用。这种规则的主要不足之处是它的输出和输出都是模糊集。然而在大多数工程系统中，系统的输入和输出都是清晰量。为了简单起见，单点模糊输出经常使用，即:

$$R^{i} : \operatorname{IF} x_{1} \text { is } F_{1}^{i} \text { and } \cdots \text { and } x_{r} \text { is } F_{r}^{i}, \text { THEN } y^{i} \text { is } C$$

其中: $C$为一个单点模糊（即清晰量）。
  以上模型简称为S模型

2 TSK模型(Takagi-Sugeno-Kang 模型)

  为了取代简单的IF-THEN规则，TSK三人共同提出了如下形式的IF-THEN规则:

$$R^{i} : \text { IF } x_{1} \text { is } F_{1}^{i} \text { and } \cdots \text { and } x_{r} \text { is } F_{r}^{i}, \text { THEN } y^{i}=a_{0}^{i}+a_{1}^{i} x_{1}+\cdots+a_{r}^{i} x_{r}$$

  其中$: F_{j}^{i}(j=1,2, \cdots, r)$是一个模糊集；$a_{j}^{i}(j=1,2, \cdots, r, i=1,2, \cdots, u)$为实值参数;$y^{i}$为根据第$i$各规则的系统的输出。
  也就是说，TSK模型考虑的规则的IF部分是模糊的而THEN部分是清晰的。它的输出是所有输入变量的线性组合，实验表面该模型具有如下有点：

• 计算效率高
• 用线性方法能够较好处理
• 用优化和自适应方法能较好处理
• 能够确保输出平面的连续性
• 更适合用于数据方法分析

---

模糊化

  精确值进入模糊推理系统时，一般要将其模糊化成给定论域上的模糊集合。模糊化的实质是将给定输入张日光模糊集合。模糊化的原则是：

• 在精确值位置模糊集合的隶属度最大
• 当输入有噪声干扰时，模糊化结果具有一定的抗干扰能力
• 模糊化运算应尽可能简单

  常用模糊化方法

• 模糊单值法
    模糊单值法是将精确值转化为模糊单值，这种模糊化方法只是形式上模糊，而实际上还是精确量。
  设$x^{}$为实测的精确值，$\tilde{A}^{}$为转换后的模糊值，则有： $$\mu_{\widetilde{A}^{*}}(x)=\left\{\begin{array}{ll}{1} & {x=x^{*}} \\ {0} & {x \neq x}\end{array}\right.$$ 优点：易于实现模糊化运算
  缺点：舍弃了所有$x \neq x^{*}$处的隶属值，因此对数据噪声的鲁棒性较差。

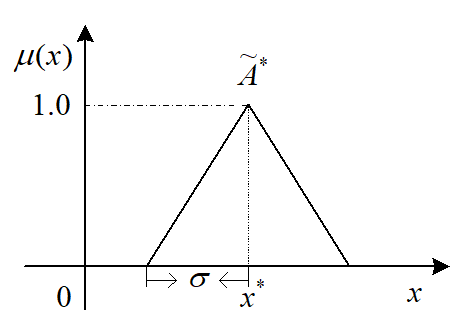
• 三角隶属函数法
    简单常用的模糊化方法，结果有一定的鲁棒性，看公式和图即可理解。$\sigma$决定了三角隶属函数的抗干扰能力。 $$\mu_{\widetilde{A}^{*}}(x)=\left\{\begin{array}{c}{1-\frac{\left|x-x^{*}\right|}{\sigma}| | x-x^{*}| \leq \sigma} \\ {0 \quad\left|x-x^{*}\right|>\sigma}\end{array}\right.$$

• 高斯隶属函数法
    与前两者相比，高斯隶属函数更常用。 $$\mu_{\widetilde{A}^{*}}(x)=e^{-\frac{\left(x-x^{*}\right)^{2}}{2 \sigma^{2}}}$$

去模糊化

  即为确定一个最能代表模糊集合的精确值。经过模糊规则后求解的仍然是模糊集合，需要经过去模糊化得到精确值。经典的去模糊化方法有：

• 最大隶属度法
    选择模糊集合中隶属值最大的点。优点是运算快，缺点显而易见，无法体现模糊集合的属性，丢失信息严重。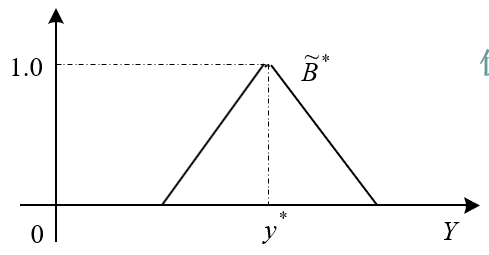
  

• 重心法（Tsukamoto模糊模型）
    加权运算得到重心位置的元素作为输出清晰值，在连续域上，计算公式为：

  $$y^{*}=\frac{\int_{y_{\min }}^{y_{\max }} y \mu(y) d y}{\int_{y_{\min }}^{y_{\max }} \mu(y) d y}$$

    在离散域上，计算公式为：

  $$y^{*}=\frac{\sum_{i=1}^{N}\left(y_{i} \mu\left(y_{i}\right)\right)}{\sum_{i=1}^{N} \mu\left(y_{i}\right)}$$

    举例：给定模糊集合：$\widetilde{C}=\frac{0.1}{2}+\frac{0.4}{3}+\frac{0.7}{4}+\frac{1.0}{5}+\frac{0.7}{6}+\frac{0.3}{7}$，其清晰值为：

  $$y^{*}=\frac{\sum_{i=1}^{N}\left(y_{i} \mu_{i}\left(y_{i}\right)\right)}{\sum_{i=1}^{N} \mu_{i}\left(y_{i}\right)}=\frac{2 \times 0.1+3 \times 0.4+4 \times 0.7+5 \times 1.0+6 \times 0.7+7 \times 0.3}{0.1+0.4+0.7+1.0+0.7+0.3}$$

Wighted Fuzzy LS

  有幸找作者要到了代码

%%初始数据
D=[ 11.5       3      2.5        0.0
    24.8       4.5    4          0.2
    40         6      7          0.4
    45.2       7      7          0.6
    49.1       9      9          0.8
    70         11     12         1.0
    70.9       12     12         1.2
    80.1       14     15         1.4
    84         15     16         1.6
    82         15     16         1.8
    103.7      16     17         2.0
    102.6      16     17         2.2
    103.1      16     17         2.4
    111        17     19         2.6
    109.1      17     19         2.8
    121.7      18     21         3.0   ];

%% 求解权重
a=0;b=0;c=0;
w=0;
n=length(D);
X=[ones(n,1) D(:,4) D(:,4).^2];
p=3;
H=X*inv(X'*X)*X';
y=D(:,1);
l=log(D(:,2));
r=log(D(:,3));

for i=1:n
w(i)=1/(max(H(i,i),p/n));
end

%W=diag(w./sum(w));
W=diag(w);
a=inv(X'*W*X)*X'*W*y;
b=inv(X'*W*X)*X'*W*l;
c=inv(X'*W*X)*X'*W*r;
Y=X*a;
L=X*b;
R=X*c;

E=(Y-y).^2+0.5*(L-l).^2+0.5*(R-r).^2;
e=sqrt(E);
M=median(e);

j=0;
E1=10;
E2=10;
E3=10;
SE=[j j j]';


while (E1>0.0001) & (E2>0.0001)  & (E3>0.0001)
j=j+1;
     for i=1:n
         w(i)=((1-H(i,i)).^2)/(max(e(i),M));
     end
%  W=diag(w./sum(w));
  W=diag(w);
  an=inv(X'*W*X)*X'*W*y;
  bn=inv(X'*W*X)*X'*W*l;
  cn=inv(X'*W*X)*X'*W*r;
  E1=abs(a-an);
  E2=abs(b-bn);
  E3=abs(c-cn);
  J=[j j j]';
  SE=[SE J E1 E2 E3]
  Y=X*an;
  L=X*bn;
  R=X*cn;
  E=(Y-y).^2+0.5*(L-l).^2+0.5*(R-r).^2;
  e=sqrt(E);
  M=median(e);
  a=an;
  b=bn;
  c=cn;
end

%% 基于权重拟合
[a b c]
W=diag(w);
an=inv(X'*W*X)*X'*W*y;
bn=inv(X'*W*X)*X'*W*l;
cn=inv(X'*W*X)*X'*W*r;
Y=X*an;
L=X*bn;
R=X*cn;

%% 无权重的拟合，用于对比
an_=inv(X'*X)*X'*y;
bn_=inv(X'*X)*X'*l;
cn_=inv(X'*X)*X'*r;
Y_=X*an_;
L_=X*bn_;
R_=X*cn_;

%% 绘图对比
plot(X(:,2), y,'b*')
text_w = string(w)
text(X(:,2), y+5,text_w)
hold on;
plot(X(:,2),Y,'b','LineWidth',2)
hold on;
plot(X(:,2),Y-L,'r','LineWidth',2)
hold on;
plot(X(:,2),Y+R,'g','LineWidth',2)
hold on;
plot(X(:,2),Y_,'k','LineWidth',2)
legend('Point','Y with weight', 'Y-L', 'Y+R','without weight')

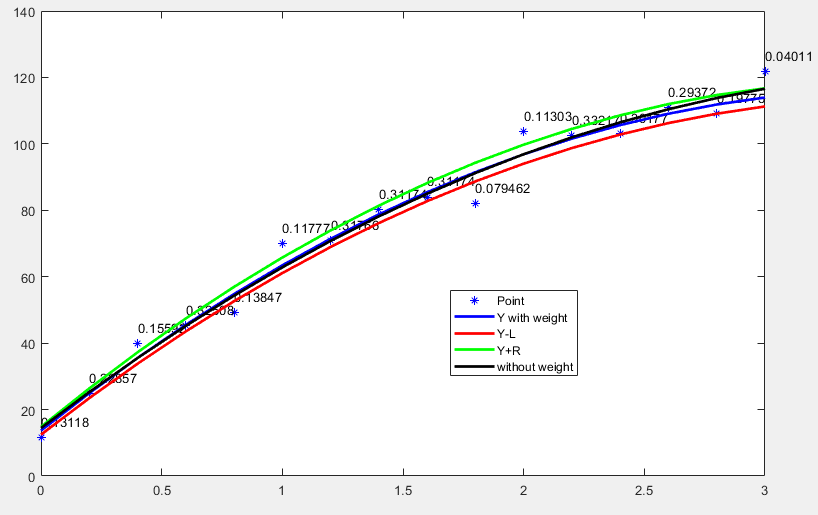
  其实模糊学习大部分时候与非模糊时效果不会有太大差异，只是从清晰数上的研究转到模糊数上，本身就是一种创新了。这层理解可能对论文研究有用