杨强的TCA 迁移成分分析(Domain adaptation via transfer component analysis),这是我认真看的第一篇计算机的论文,感觉有点吃力,其实网上有一些解读,只是我的底子比较差,没怎么看懂。看完这个文章再看其他的才发现,距离函数、核运算都是的基本知识,路漫漫啊。
TCA:迁移成分分析
步骤1:将源数据和目标数据都映射到希尔伯特空间中,在此空间中两数据源距离最近,求矩阵$K$。
步骤2:定义低维的矩阵$W$,结合约束优化$W$。这个W就是“迁移成分”。
解释:
步骤一其实是杨强的另一篇论文,用半正定规划求解映射$K$。
(Pan S J, Kwok J T, Yang Q. Transfer learning via dimensionality reduction[J].2008, 2:677-682.)
步骤二为了得到W其实并没有优化K,本文实验中是把步骤一的映射假设为线性核或者高斯核。
步骤1:基于MMD定义优化目标
对于源数据样本$X_{s}$,目标数据样本$X_{T}$,定义距离函数,最大均值差异(MMD,maximum
mean discrepancy):
式中$n_{1}$和$n_{2}$,分别$X_{s},X_{t}$的样本个数。式(1)展开可表示为:
即为$n_{1}$+$n_{2}$个元素累加平方,共${(n_{1} + n_{2})}^{2}$个元素。即为:
此时,定义核函数[1]$K:x$
即$K = \left\lbrack {\phi\left( x_{i} \right)}^{T}\phi\left( x_{j} \right)\right\rbrack,i,j\in \lbrack 1,n_{1} + n_{2}\rbrack$,即为$(n_{1} + n_{2})\times (n_{1} +n_{2})$的内积矩阵,上展开式即为这些内积矩阵再乘上系数(即为上展开式中有颜色的部分),因此再定义一个系数矩阵L:
再定义$L$:
设展$n_{1}$=3和$n_{2} = 2$,则矩阵展开为:
因此矩阵K的每行乘以矩阵L的每列,再相加,即为式(3),因此式3可以描述为矩阵的迹[2](矩阵的迹即为对角线元素相加)
在MMDE【Transfer Learning via Dimensionality Reduction】文中解释了,为了保持两个域中的数据的特性,引入【2006 Colored Maximum Variance Unfolding】文中提出的MVU(最大方差展开),就是说最大化$\operatorname{tr}(K)$可以达到保持两个域中数据特性的效果。于是距离函数定义为:
这里为什么要最大化$\operatorname{tr}(K)$其实并没有严格证明,只是在降维迁移文中直接给出了这个结论,在后面公式中有事并没有考虑这一项,因此推测这一项并不重要。
此时,我们的优化目标可以定义为:
个人理解:到这里其实是杨强之前一篇论文[5],原文式(8)中的K是用半正定规划[6]强行求解的,求解之后是用PCA进行降维,这个求解过程对我们可能有帮助,而本文TCA并没有求解K,在算法操作过程中直接定义核函数(线性核或者高斯核)。
步骤2:降维定义新目标函数(Parametric Kernel Map for Unseen Patterns)
首先核矩阵可以表示为经验核映射 empirical kernel map ,$K$矩阵是正定矩阵,可以分解为$K=(K^{1/2})^2$
此时$K$是($n_{1} + n_{2}$)维,为了将核矩阵降为$m$维($m <n_{1} + n_{2}$),定义一个矩阵$\tilde{W} \in \mathbb{R}^{(n_{1} + n_{2})\times m}$,此时构造一个新的核矩阵可以表示为:
其中${W = K}^{- \frac{1}{2}}\tilde{W}$, 此时距离函数变为:
此处用到了迹运算的性质$\operatorname{tr}(\mathbf{A B})=\operatorname{tr}(\mathbf{B} \mathbf{A})$。
在MMDE文中,首先SDP求解核矩阵$\mathbf{K}$,使用的时侯是把核矩阵PCA降维。相当于降维的时侯并没有用MMD约束,所以后面作者应该想,如何使降维过程也用MMD约束呢,于是就演变成了这个文章。
构建好新的核矩阵之后,最终训练的时侯可以用$\mathrm{KW}$也可以用$\mathrm{W}$作为训练数据,两者的维度都是$m$。
此时,目标函数定义为:
其中$\text{tr}\left( W^{T}W\right)$作为惩罚项来降低$W$的复杂度,这个是可以理解的。
原文中说正则项作用还有“avoid the rank deficiency of the denominator in the generalized eigenvalue decomposition“,翻译过来是”在广义特征值分解过程中避免分母秩亏“。
是不是现在就可以得到完美的降维域移植呢,不是的,请看以下两点现象:
观察现象:
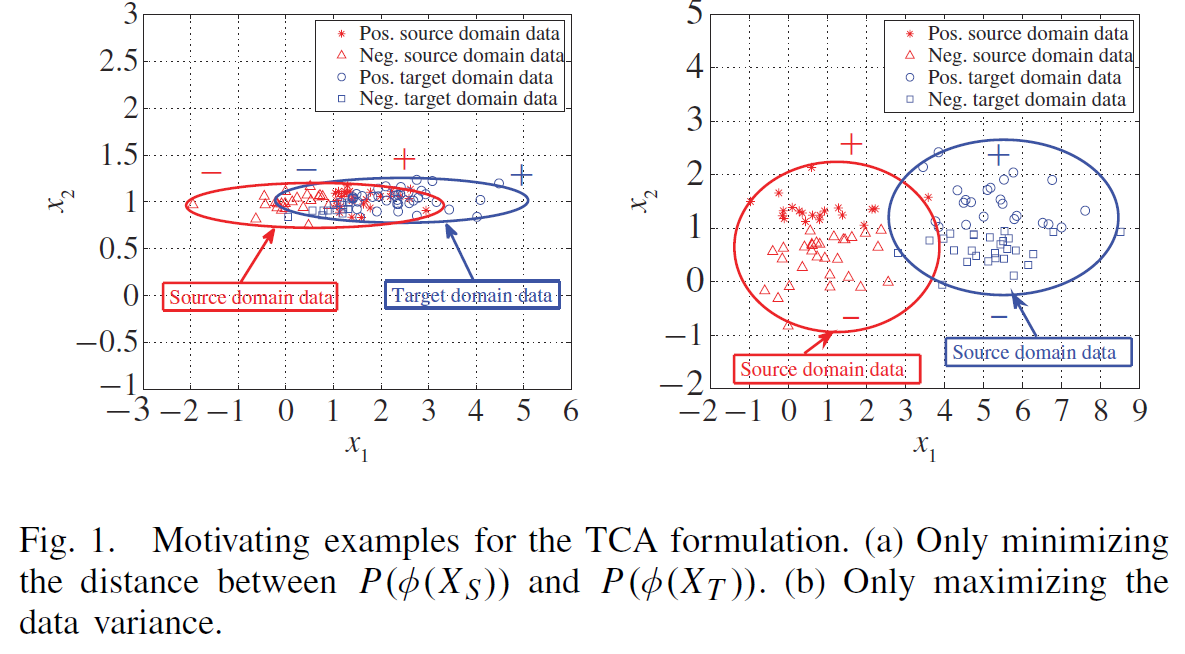
(a)距离函数本身要能够体现数据的特征,我们希望映射之后的数据距离更近但本身的散度要保持,如下图(a),分类对$x_{1}$方向敏感,而$x_{2}$方向只是随机噪声,然而按照距离求解核矩阵时,映射可能把$x_{1}$方向的大跨度压缩,而试图优化$x_{2}$方向的距离,这样虽然可以使距离小,却由于丢失$x_{1}$方向的散度导致结果对分类任务没有帮助。因此映射要保持数据本身各个维度的散度特征。
(b)然而有时过多注重保留散度也不好,如图(b)$x_{1}$方向的散度很大但是对分类其实没有用。
步骤3:在体现数据散度特征的同时优化W
一组数据的散度可以用散列矩阵(Scattermatrix)来描述,对于一个矩阵A,其散度可表示为:$S =\text{AH}A^{T}$,其中$H$为中心矩阵[7],对于式(10),数据经过改进的核矩阵已经表示为$W^{T}K$,因此其散度可以表示为$W^{T}K\text{HKW}$,其中$H= \mathbf{I}_{n_{1} + n_{2}} - \frac{1}{nn_{1} +n_{2}}\mathbf{11}^{T}$,其中$\mathbf{I}_{n_{1} + n_{2}} \in \mathbb{R}^{(n_{1}+ n_{2}) \times m}$
是单位矩阵。为了保持源数据各个维度的散度特征不变,上述优化问题可以表示为
其中$\mu$是正则化控制参数。式(11)为约束条件,保持散度不变。
首先可以用拉格朗日法转化成优化目标:
其中的$Z$为对角矩阵,对角线为拉格朗日算子。为了使得上式最小,对$W$求导,然后使得导数为零即可:
然后令$A={(KLK+\mu I)}^{-1}KHK$,则上式表示为:
这个式子$W$的解显然为$A$的前$m$个特征向量。结论是,$W$的解即为${(\text{KLK}+ \mu I)}^{- 1}\text{KHK}$的前m个特征向量。
SSTCA:半监督迁移成分分析
考虑源数据有Y标签,因此可以采用半监督,主要基于Hilbert–Schmidt Independence
Criterion (HSIC),并添加了约束如下:
(1)减小源数据和目标数据的在嵌入空间中的分布距离(基于MMD,自己随便定义一个核)
(2)保持标签独立性(不懂为何可以实现)
其中$K_{l}$为标签的核,目标数据部分为0。
(3)维持数据流形相似下降维
依据:如果两个数据$x_{1}$和$x_{2}$在源空间中距离相近,我们希望在嵌入空间中两者距离依然相近,这就是维持数据流形。采用的方法是拉普拉斯映射[8],在源空间中$x_{1}$附近$k$个数据定义为相邻,其系数定义为$m_{\text{ij}}= exp( -d_{\text{ij}}^{2}/{2\sigma}^{2})$,根据相邻点和权重定义度矩阵D和邻接矩阵M,即可定义拉普拉斯矩阵$\mathcal{L}= D -M$,对于嵌入数据$\mathcal{A}$矩阵拉普拉斯矩$\mathcal{L}$阵有个性质[9]如下:
这个性质证明见参考文献。由于我们问题中嵌入数据是$W^{T}K$,因此优化目标为控制嵌入空间中的距离加权和最小即为:
到此,把多个约束加在一起,再上点正则化项即可:
其中$\lambda$和$\mu$都是正则化控制参数。
其中W的解刚好是${(K\left( L + \lambda\mathcal{L} \right)K + \mu I)}^{-1}\text{KH}{\tilde{K}}_{\text{yy}}HK$的前m个特征向量。
实验对比方法可以学习学习,多维度进行了对比。
生成数据对比
(1)只优化距离,SSA
(2)只保持散度进行降维:PCA
(3)SSTCA
(4)只保持流形进行降维:双月流形结构
基于wifi信号定位回归问题
(1)实验准备:a.传统回归模型 RLSR b.传统降维模型 KPCA
c.传统的调整权重训练KMM和KLIEP d.现有的领域适配 SCL e.本文的TCA和SSTCA
f.只优化距离不保持散度 SSA TCAReduced g.最新的降维方法 MMDE
(2)与其他降维方法对比: b g d f
(3)与传统方法对比: a b e
(4)与域移植方法对比:c d e f
(5)与MMDE相比(因为这个方法是杨强自己提出的)
(6)对参数的敏感性
文本分类问题
对比同B
[1]: 核函数定义(来自《统计学习方法》)设$\mathcal{X}$是输入空间(欧式空间$\mathbf{R}^{n}$的子集或者离散集合),又设$\mathcal{H}$为特征空间(希尔伯特空间),如果存在一个从$\mathcal{X}$到$\mathcal{H}$的映射:$\phi\left(x\right):\mathcal{X \rightarrow}\mathcal{H}$,使得对所有$x,z \in\mathcal{X}$,函数$(x,z)$满足条件:$K\left( x,z \right) = \phi\left( x\right) \bullet \phi\left( z \right)$,则称$K\left( x,z\right)$为核函数,式中$\phi\left( x \right) \bullet \phi\left( z\right)$为$\phi\left( x \right)$和$\phi\left( z\right)$的内积。当映射$\phi$$难以显示表达的时候,用核函数方便计算。
[2]: 矩阵的迹:一个n×n矩阵A的主对角线上各个元素的总和被称为矩阵A的迹记作tr(A)
[3]: 李航. 统计学习方法[M]. 清华大学出版社, 2012.
[4]: Song, L. 2007. Learning via Hilbert Space Embedding of Distributions.
Ph.D. Dissertation, The University of Sydney.Draft.
[5]: Pan S J, Kwok J T, Yang Q. Transfer learning via dimensionality
reduction[J]. 2008, 2:677-682.
[6]: Lanckriet G R G, Cristianini N, Bartlett P, et al. Learning the Kernel
Matrix with Semidefinite Programming[J]. Journal of Machine Learning Research,
2002, 5(1):27-72.
[7]: 中心矩阵:若$A \in \mathbb{R}^{n}$,则$H = \mathbf{I}_{n} -
\frac{1}{n}\mathbf{11}^{T}$,称做n阶中心矩阵。举例:当$n = 3$时:
[9]: Belkin M, Niyogi P, Sindhwani V. Manifold Regularization: A Geometric
Framework for Learning from Labeled and Unlabeled Examples[J]. Journal of
Machine Learning Research, 2006, 7(1):2399-2434.