1. 离散卡尔曼滤波

待估计的过程

卡尔曼滤波解决的是离散控制过程状态估计问题，状态$x \in \Re^{n}$， 系统由线性随机差分方程控制：

  博客基于Hexo，主题基于Next，这里记录一些重要操作。

衡量分布距离在机器学习算法中非常常用，然而分布估计往往运算量大，又不够准确。将分布映射到RKHS上，可以带来很好的性质，因此本篇介绍一下分布嵌入算子，包括边缘嵌入算子，条件嵌入算子和联合嵌入算子。

如果我们定义了一个观测变量和隐变量的联合分布，那么观测变量的分布就可以通过对隐变量边缘化得到，也就是把隐变量积分掉。因此，可以把难以求解的观测变量的边缘分布扩展至一种相对容易处理的方式，即扩展到由观测变量和隐变量构成的联合分布，潜变量的引入可以把复杂的分布拆解成简单的分布。

数学运算

矩阵点乘，即对应元素相乘

1
2
3

numpy   : A * B 
matlab  : A.*B
pytorch : A.mul(B)

矩阵运算相乘，即 $A\in{R^{n\times m}},$ $B\in{R^{m\times n}}$, $AB\in R^{n\times n}$

1
2
3

numpy   : np.dot(A, B) 
matlab  : A*B
pytorch : A.mm(B)

操作

查到数组中大于3的元素及索引

1
2
3

numpy   : out = [i for i, x in enumerate(e) if x > 3]
matlab  : out = find(e > 3)
pytorch : out = e[e.gt(3)] # gt大于 lt小于  eq等于

Source-Target Similarity Modeling

2010 Cao 提出了单源数据的transfer covariance function,本文将其称作$TC_{\text{SS}}$，基于此的迁移学习方法就叫做$\text{GP} -
TC_{\text{SS}}$。本文针对的是多源问题，就是$TC_{\text{MS}}$，直观上，可以对每个源都按照$TC_{\text{SS}}$去构造，但是本文证明直接利用是不可行的。本文提出了Stacking的方法。

- The Adaptive Transfer Learning Model via Gaussian Process

AAAI Adaptive transfer leanring 为了使得源和目标任务之间能迁移知识，我们首先要定义两者之间的联系。一种方式就是使源和目标的核函数共享一些相同的参数$\mathbf{\theta}$，核函数代表了平滑性，共享核函数参数意味着两任务回归函数的平滑性相似。另一些方法利用了数据输出之间的关联性【这个可以关注一下】。本方法是半参数化，构造了任务之间的相似性和样本之间的相关性

  高斯过程回归是一种基于贝叶斯的回归方法，有点难以捉摸，上一篇笔记从公式角度推了，这一篇从图的角度看看什么是高斯过程，如何进行高斯过程回归的，看到一篇国外博客说的很好，于是翻译了过来。参考见文尾。

  GP回归对多源回归迁移作用很大，因此现在好好学一下。高斯过程回归的加权理解整体做法是，根据少量观测值，预测某组参数的似然概率，然后对所有可能的模型按照概率进行加权，所以这一节定义为’weight-space view’，就是高斯过程回归的加权空间解释。其认为出输出是各种输入的可能性叠加。模型输入包括噪声的方差$\sigma_{n}^{}$，以及参数的协方差矩阵$\Sigma$，输出是带有方差和均值的结果。这个方法整体还是线性的，表现力肯定有限。

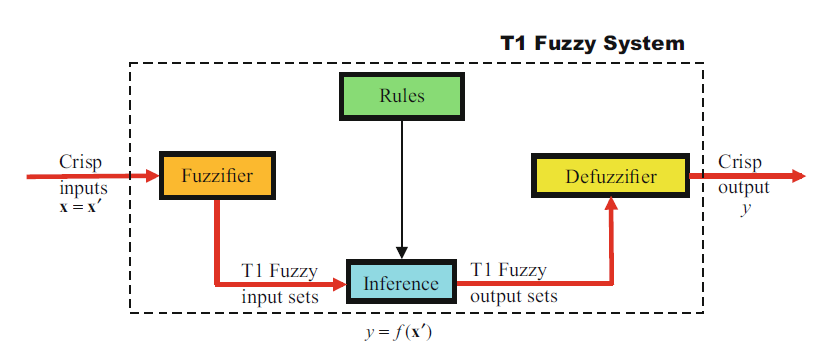
  首先开始学习Type-1 fuzzy system (T1 FS), 详细的书中都有，因此这里只从个人理解的方式讲，并非系统学习。T1 FS包括模糊器(Fuzzifier)、推理机(Inference)、规则(Rules)和解模糊器(Defuzzifier)。